On the 11th and 12th of September I helped students from the Sint-Oelbert Gymnasium to measure a meander of the river Geul in the vicinity of Epen. The project is part of the school’s scientific week in which the students are introduced to the scientific method. Throughout the week students participate in projects that revolve around biology, geography, chemistry, social sciences and philosophy. They define a hypothesis, perform experiments and collect data, analyse their findigs, draw conclusions and present the results to each other.
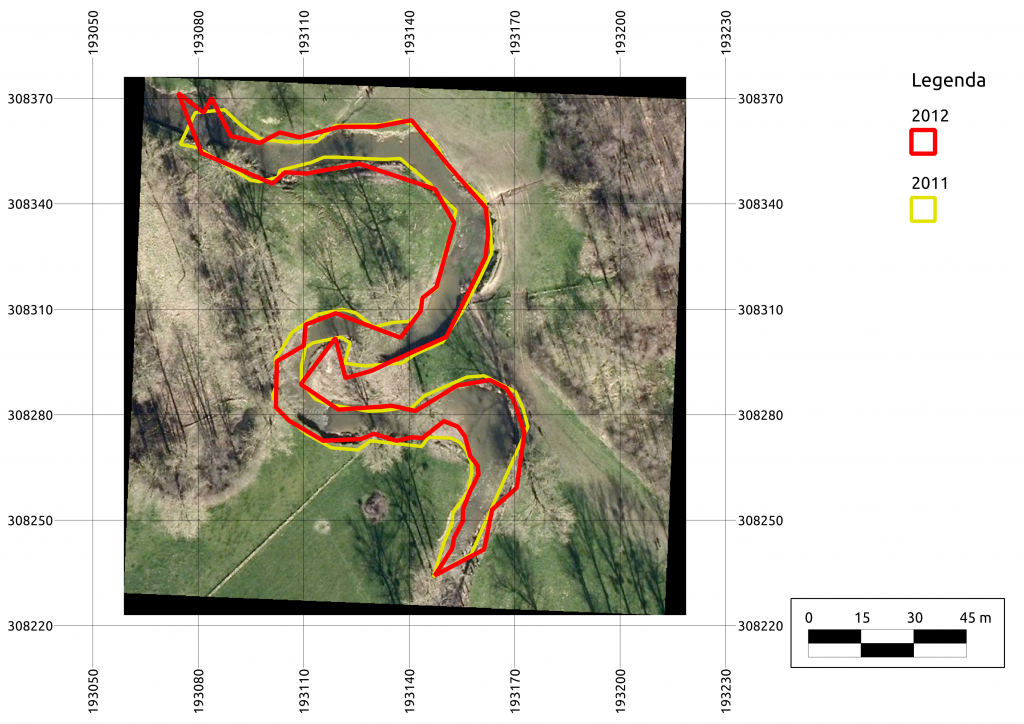
I helped with the geography project that consisted of surveying the meander shown below and, based on measurements from previous years, coming up with a plausible prediction of the meander’s future developments.
Two competing hypotheses are set forth: the first states that the river will breach the embarkment to the west of the green arrow and flow into the small forest. This hypothesis is somewhat plausible as there lies an old river bed that is the result of past river flows. The second hypothesis states that the river will breach the piece of land that sits between the two flows (under the green arrow). This is the likely outcome: a tree fell into the river last year and completely readjusted the flow.
Besides teaching the kids how to do science and perform measurements, the surveying exercise also aims to spark an interest in mathematics, Geomatics and engineering at large. It also aims to demonstrate that the map is not the territory. This issue quickly presents itself once the students start measuring: what is the extent of the river? Do we measure the up to the water border or beyond? What if the water level is higher than normal due to rain? Do we come back to measure again? What do you do when you cannot measure a certain stretch because it is inaccessible?
Setup and measurements
The measurement set-up consisted of three total stations the locations of which are determined by high-precision GPS. A total station is an electronic/optical instrument that measures distances and (relative) angles. Distances are measured by emitting an electromagnetic signal that is reflected by a prism reflector. An object, in this case the river, is measured by moving the reflector alongside the river’s bank and performing point measurements.
The measurement are executed by a team of three students: two students operate the total station while the third walks the scene with the reflector. At first the students are uneasy with the instrument, each other and the water. But as soon as the first couple of measurements are completed a comfortable atmosphere descends on everybody and all goes smooth and elegant: students conquer their fear of water, they start to communicate with each other, and take turns operating the instrument and walking the reflector.
At the end of the afternoon they produced a list of distance/angle measurements which they, most clumsily, punched into a CSV file on my computer.
Making a map
This is the part in which I get to sprinkle some GIS/coding magic dust on the day and collect some ‘Oohs’ and ‘Aahs’. I parsed the students’ measurements and did some simple trigonometry, fetched and georeferenced a Google Maps image and plotted their measurements on a map using QGIS. The resulting map, although very simple, did not fail to impress (primarily because it was crafted before their eyes). The students were excited to see the day’s work on the screen (in what I imagine to be a minor disbelief at the so-emerging connection between their physical effort and the stuff on the screen).
Plotting the measurements from the previous year releases a torrent of revelations: everybody hurries to look for differences between both datasets but quickly realizes that one-on-one comparisons are difficult. Are the difference explained by measurement errors or real changes in the river bed? What about differences between the underlying image and the two datasets? At first the image is taken for the truth; if a measurement does not align with it, surely the measurment must be wrong. A short silence marks the readjusment of their mental maps when I tell them the image is older, no idea how old exactly, than their measurements. The analyses that follow are of a higher complexity; differences between the two datasets are coupled to the plausability of their correctness i.e. does the position and value of a measurement rhyme with river flow theory. All in all it was great to hear them debate the results.
Fortunately the measurements fully support the second hypothesis. The fallen tree diverts the flow such that erosion is quickly eating away the soil between the two turns. The map shown below displays the fallen tree (brown line) and the resulting erosion to the south of it.
Why help out?
Last year our primary mission was to promote the MSc Geomatics to the 4th graders with the hope that they’ll choose to study it in 5 years. We showed them 3D (urban) models, a range camera and explained that total stations are somewhat outdated when it comes to obtaining massive amounts of data. I am very fond of Geomatics and gladly accepted this opportunity to spread some Geo enthusiasm.
Another reason to help last year was that, despite being a Geomatics engineer, I had not seen a total station and was curious to understand how one works and perform measurements with it.
But what really made me come back were the students themselves: they are extremely smart, enthusiastic, work hard and are willing to learn new things. Working with them was a joy.
Throughout my last MSc year I had to explain and teach simple things to fellow students. I realized that I enjoy educating others; translating a complex concept in a simple tangible example that someone else understands is difficult but very rewarding, especially when the other person eventually grasps your explanation and runs away with it. During this year’s scientific week in Epen I wanted to make sure that teaching is more than a fleeting sensation for me..
..it turns out it is; so much so that last week I went on a weeklong post-summer school to Bulgaria to teach 1st year MSc students what it is we do at the Geomatics group at Delft University of Technology. A blog post about that adventure is forthcoming!